Astronomy and the approach to mathematical modeling

Under this context of observation, the existence in the galaxy of physical phenomena is verified, arising with it great unknowns as the constancy of the speed of light, which at the same time refers to the transformation of mass into energy, as also the scientist tries to build models of more accurate units, to be applied in the case of distances in the universe, the most used is drawing points and applied the equation of the straight line, to establish a geometry on the star, the solar system and galaxies.
Thus I established the following philosophical comparison on this subject with different authors:
Carl Freidrich Gauss (1777-1855), German mathematician is known as the prince of mathematics, considered one of the greatest mathematicians of all time, was the creator of one of the most widely used systems for the solution of systems of linear equations. During his life, Gauss ventured into many areas of mathematics, physics and astronomy. Spiral 9 By William Fernando Estrada García page 103. | Galileo not only established that through mathematics it was possible to describe the laws of the world, but also stated that the first principles, those from which the laws had to be deduced mathematically, had to be established through experience and experimentation. If it is well understood, this methodology, which affirms mathematical experience and quantification in the description of external reality, possessed a revolutionary force even more profound than any revolution in cosmology. Historia Y Filosofía de Las Matemáticas by Ángel Ruiz Zúñiga page 255. |
All these contributions are valuable, to understand more the universe and the way astronomy approaches it, we can also add that generalized law, mentioned in the scheme of Descartes, where he uses his experiences with the inclined plane, in order to modify the acceleration with which a serious falls, then let's see from the point of view the theory of the "Big Bang". On the other hand it is important to be documented, to learn more about knowledge of this height.
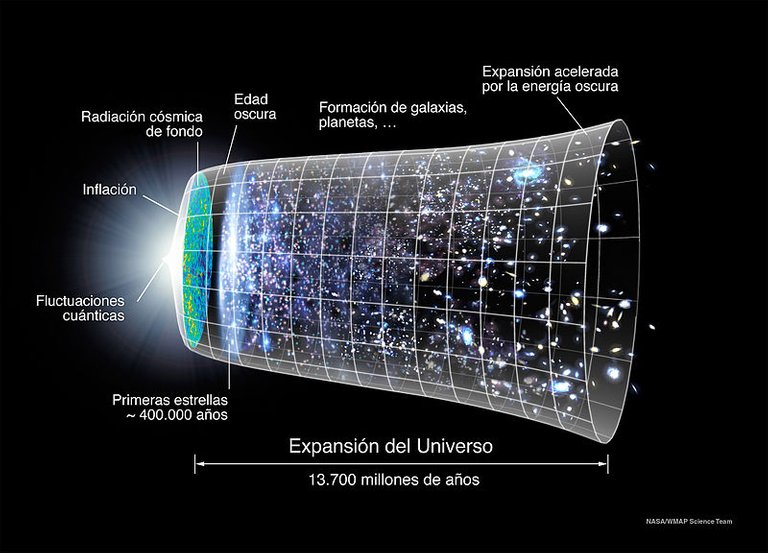
Ilustración de la teoría del "Big Bang" o primera gran explosión y de la evolución esquemática del universo desde entonces, fuente de imagen de dominio de Wikimedia Commons, Fecha: 13 de septiembre de 2015, Fuente File:Evolución Universo WMAP.jpg, File:CMB Timeline300 no WMAP.jpg, Versión original: NASA, Autor: NASA, Ryan Kaldari, adaptación al español: Luis Fernández García, borrado del WMAP: Basquetteur
Para este caso compañeros el abordaje matemático va estar definido en abarcar el estudiar la evolución del universo, en función de la magnitud del tiempo y espacio, ya que la gravedad actúa de diferente afectando la densidad de la materia, ya está emite energía. Considerando que muchos de estos fenómenos, experimenta radiaciones menores de la velocidad de la luz, podemos establecer lo siguiente tomamos una esfera de una estrella el cual tiene un radio R, al mismo tiempo esta tiene una densidad constante r, donde su masa se mueve en espacio tiempo en una misma gravedad m.
For this case, the mathematical approach will be defined in the study of the evolution of the universe, depending on the magnitude of time and space, since gravity acts differently affecting the density of matter, since it emits energy. Considering that many of these phenomena, it experiences radiations smaller than the speed of light, we can establish the following we take a sphere of a star which has a radius R, at the same time this one has a constant density r, where its mass moves in space time in a same gravity m.
As we are considering a constant density we have the following: E = 1/2 m v2 - 4/3 p G m m r R2
With this mathematical approach, we tried to explain under the relativistic concept, how we can try to dogmatize that the total energy of the Galaxy. This is a small contribution, since there is more theory on the subject.
Birkoff's Theorem
Therefore, given that the Newtonian gravitational potential on the outside of a spherical distribution of mass m is given by:
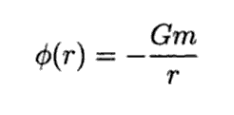
And the component for the Schwarzschild metric is:
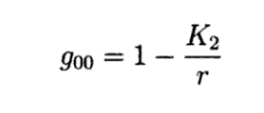
Then:
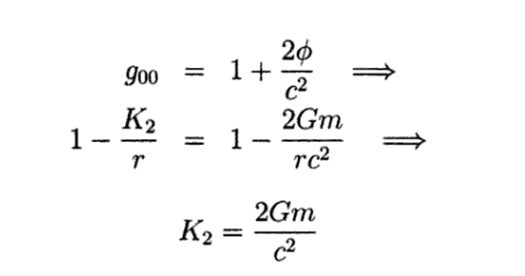
Thus, the Schwarzschild metric is given by:
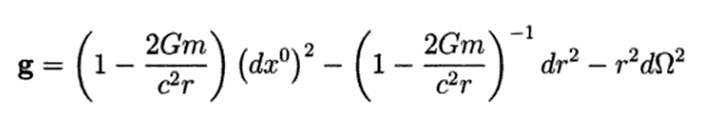
The method used to calculate the integration constant K2, even if it leads to the correct result, leaves open the question of the physical interpretation of the mass as the source of the field, through the momentum-energy tensor. For this purpose it is necessary to develop the gravitational field. Lecture notes. Principles of general relativity by Juan Manuel Tejeiro Sarmiento, pages 133, 134..
It is important to say, that the mathematical approach has a lot of application in our life, in the case of our subject of astronomy, what is tried as much as possible, is that the studies are dynamic about the universe as a whole and its evolution in time and space, waiting for something new to happen in it.
Bibliographic Consultation used
Spiral 9 - Page vii William Fernando Estrada García.
History and Philosophy of Mathematics - Page 255 by Ángel Ruiz Zúñiga - 2003.
Class Notes. Principles of General Relativity
By Juan Manuel Tejeiro Sarmiento pages 133, 134, 2005.
